UNIDAD III
ÍNDICE
1.-Matrices
1.-MATRICES
1.1-SUMA
DE MATRICES
Para sumar dos matrices A y
B han de ser de las mismas dimensiones; si esto es cierto, la suma es una
matriz E de iguales dimensiones que A y que B, y sus elementos se obtienen sumando
los elementos correspondientes de A y B.
1.2
PRODUCTO DE MATRICES POR UN ESCALAR
Así como se ha definido la suma de matrices,
también se puede formar el producto de un número real Α y una matriz A. El resultado, denotado por Α A, es la matriz cuyos elementos son los componentes de A
multiplicados por Α.
1.3 MULTIPLICACIÓN
DE MATRICES
Dos matrices A y B son conformes en ese orden (primero A
y después B ), si a tiene el mismo número de columnas que B tiene de filas.
2.- VECTORES
2.1
suma de vectores
Agrupando términos:
2.2
resta de vectores
Ejemplo
resta:
2.3 Producto
de Vectores
El producto escalar de dos
vectores no es otro vector sino un número. Se determina multiplicando las
coordenadas de ambos vectores, componente a componente y sumando los
resultados.
CLASIFICACIÓN DE UN SISTEMA SEGÚN EL NÚMERO
DE SOLUCIONES
SISTEMAS
EQUIVALENTES
Dos sistemas de ecuaciones
lineales son equivalentes si tienen exactamente las mismas soluciones.
Transformaciones que
convierten un sistema en otro equivalente:
I.- Multiplicar
o dividir ambos miembros de una ecuación por un número distinto de cero.
II.- Sumar
a una ecuación del sistema otra ecuación del mismo.
III. Eliminar
una ecuación que es combinación lineal de otras dos.
RESOLUCIÓN
DE SISTEMAS DE ECUACIONES
Resolver un sistema es
encontrar todas sus soluciones o decidir que no tiene ninguna.
Métodos de resolución:
Método de Gauss.
Resolver un sistema es
encontrar todas sus soluciones o decidir que no tiene ninguna.
Un sistema equivalente y escalonado, mediante transformaciones adecuadas.
Se pueden dar los siguientes pasos:
I. Si es necesario reordenar ecuaciones para que a11 sea distinto de cero.
II. Dividir la primera ecuación por a11 y restar a cada ecuación un múltiplo de la primera para eliminar todos los elementos que quedan por debajo de a11x1.
III. Repetir los pasos anteriores basados ahora en a22 (y si es necesario en cada aii).
IV. El proceso termina cuando no quedan más ecuaciones.
Método de Cramer.
Esta regla establece que cada incógnita de un sistema de ecuaciones lineales algebraicas puede expresarse como una fracción de dos determinantes con denominador d y con el numerador obtenido a partir de d, al reemplazar la columna de coeficientes de la incógnita en cuestión por las constantes b1, …b2,…, bn. por ejemplo, x1 se calcula como:
Ejemplo:
DESCOMPOSICIÓN
LU
Recordemos, que una matriz
regular a, admite una factorización de la forma
Pa=lu
Donde p es una matriz de
permutación de filas, l es una matriz triangular inferior y u es una matriz
triangular superior. Y sea el sistema de ecuaciones [a][x]=[b] aunque la eliminación
gauss representa una forma satisfactoria para resolver tales sistemas,
Resulta ineficiente cuando
deben resolverse ecuaciones con los mismos coeficientes [a], pero con
diferentes constantes del lado derecho (las b). Los métodos de descomposición lu
separan el tiempo usado en las eliminaciones para la matriz [a] de las
manipulaciones en el lado derecho {b}. Una vez que [a] se ha “descompuesto”,
los múltiples vectores del lado derecho {b} se pueden evaluar de manera
eficiente.








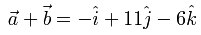










No hay comentarios:
Publicar un comentario